Simulation à l’échelle nationale du mouvement humain dans un modèle individuel couplé spatialement du paludisme au Burkina Faso

Modèle mathématique

Le succès général et l’application des modèles de gravité pour le mouvement humain et la migration en ASS^8,9couplé avec les travaux récents de Marshall et al.^8,17nous a motivés à commencer avec le modèle de gravité modifié suggéré :

où \({\text{Pr}}(j|i)\) décrit la probabilité de voyager depuis la source je à destination jétant donné le produit de la population de j élevé à τ (Eq. 1), et le noyau de distance (Eq. 2), qui prend la forme d’une loi de puissance contenant le paramètre d’échelle ρet le paramètre de loi de puissance α.

Deux limites sont présentes dans le modèle construit par Marshall et al.⁸ Premièrement, le modèle suppose qu’une destination entière (c’est-à-dire une ville de destination) peut être traitée comme un point, ce qui entraîne une incongruité lorsqu’elle est utilisée dans le contexte d’un paysage basé sur une grille. Deuxièmement, le manque de considération pour le temps, la distance ou la complexité du voyage vers une destination donnée. Ceci est particulièrement important dans le contexte des interventions contre le paludisme, car les communautés rurales peuvent manquer de ressources médicales locales, ce qui nécessite des déplacements pour se faire soigner.^5,23. En conséquence, cette limitation peut être résolue en capturant la difficulté associée au déplacement grâce à l’utilisation d’une surface de friction, qui quantifie la facilité ou la difficulté à traverser des surfaces (par exemple, des types de route) ou des barrières naturelles telles qu’un terrain montagneux.²⁴. Une alternative est l’utilisation d’une carte de temps de trajet (ou surface) qui estime le temps pour atteindre la ville la plus proche (ou la zone urbaine à haute densité) à partir d’un emplacement donné sur la carte²⁵. Étant donné que les cartes de temps de trajet annotent généralement le temps de trajet dans un environnement urbain comme étant nul, cela résout également l’incongruité qui survient puisque les limites urbaines sont délimitées par des temps de trajet nuls.

En conséquence, la probabilité de mouvement peut être ajustée pour utiliser les temps de trajet comme suit :

où \({\text{Pr}}(j|i)\prime\) décrit la nouvelle probabilité de voyager depuis la source je à destination j suivant la division de la probabilité originale \({\text{Pr}}(j|i)\) par la somme de un plus le temps de trajet jusqu’à la ville la plus proche de la source t_je et destination t_j. Incorporation à la fois de la source t_je et destination t_j au dénominateur de l’Eq. (3) assure la comptabilisation des coûts des trajets indirects. Cela a pour effet de biaiser le modèle vers les cellules de destination qui sont situées dans (c’est-à-dire, un temps de trajet de zéro) ou à proximité (c’est-à-dire, un temps de trajet faible vers la ville la plus proche) des villes, mais qui permettent toujours des déplacements entre des zones rurales ou depuis la ville vers une zone rurale. Notez que puisque les déplacements à l’intérieur d’une ville ne sont pas pénalisés (c’est-à-dire que le temps de trajet de la source et de la destination est égal à zéro), lors de l’étalonnage du modèle, il faut veiller à ce que le nombre de déplacements (par exemple, à l’intérieur d’une ville ou d’une province, ou entre des villes ou provinces) sont correctement pris en compte. Si nécessaire, \({\text{Pr}}(j|i)\prime\) peut être ajusté en divisant par un paramètre de pénalité, pdans le cas où le modèle est biaisé en faveur d’un mouvement restant dans une zone donnée.

Évaluation du modèle mis en œuvre

Le modèle mathématique développé, c’est-à-dire les équations. (1–3) – a été implémenté dans le cadre d’un IBM stochastique développé pour le Burkina Faso^6,26et la paramétrisation des équations de mouvement a été effectuée en estimant d’abord le meilleur ajustement pour le ρ basé sur le \(log_{e} \left( \rho \right)\) de la gamme de valeurs suggérées par Marshall et al.⁸avec \(log_{e} \left( \rho \right) = 0,20\) ayant le meilleur ajustement aux données de l’enquête¹⁷. Ensuite, les valeurs déduites \(\alpha = 1,27\) et \(\tau = 1,342\)selon Marshall et al.⁸, ont été utilisés dans un IBM du Burkina Faso pendant un mois avec une population d’environ 19 millions d’individus, et tous les déplacements entre les cellules ont été enregistrés. Le mouvement cellulaire de la simulation a été agrégé au niveau de la province et comparé à celui de Marshall et al.¹⁷ données de l’Enquête. Les premiers résultats du calibrage ont révélé un biais du modèle dans la province de Kadiogo – contenant la capitale Ouagadougou – en raison du mouvement individuel restant dans la province en raison de la forte population par rapport au reste du pays. Ceci a été corrigé en divisant Pr’ par la pénalité du modèle \(p ​​= 12\) lorsque la cellule se trouve dans la province de Kadiogo, où la valeur de la pénalité a été trouvée grâce à l’ajustement du modèle. En conséquence, il a été constaté que la probabilité de mouvement \({\text{Pr}}(j|i)\prime\)couplé à une pénalité modèle appliquée à la province de Kadiogo, produit une réplication raisonnable du mouvement de la source à la destination dans les régions du Burkina Faso à forte population géographiquement dispersée (Fig. 3).

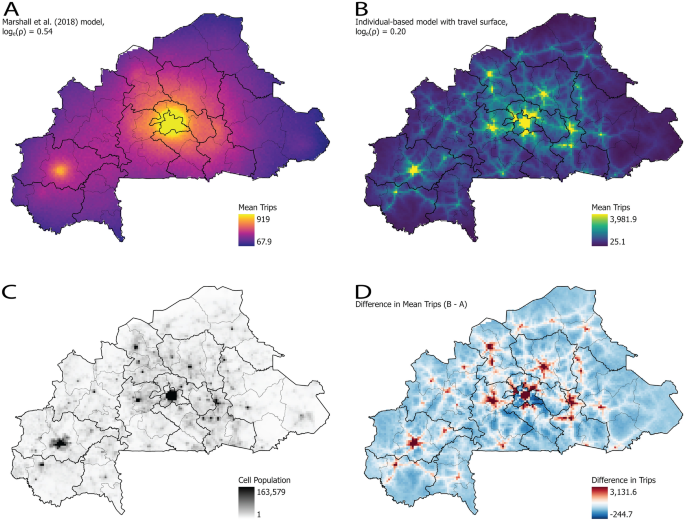
Comparaison du modèle de gravité avec la fonction noyau paramétrée par Marshall et al.⁸ versus le modèle mathématique avec surface de déplacement et paramétrage décrit, tel qu’implémenté dans le modèle individualisé. (une) Le nombre moyen de voyages pour dix répétitions vers la cellule de destination en un seul mois en utilisant la paramétrisation préparée par Marshall et al.⁸ (b) Le nombre moyen de voyages pour dix répétitions vers la cellule de destination en un seul mois en utilisant le modèle mathématique avec surface de déplacement et paramétrisation décrit dans ce manuscrit. (c) La répartition de la population du Burkina Faso d’après WorldPop¹⁸ regroupées dans les mêmes cellules de 5 km sur 5 km utilisées pour le déplacement. (ré) La différence d’algèbre raster entre le nombre moyen de trajets vers la cellule de destination depuis (une,b); noter que le Marshall et al.⁸ modèle tend à projeter un déplacement plus important vers les zones rurales (valeurs négatives dans les tons bleus) par rapport à (b) qui est décalée vers les zones les plus peuplées selon la méthode décrite ici (valeurs positives dans les tons rouges). De plus, le mouvement est moins diffus par rapport à (une). Cependant, le manque de diffusion fait en sorte que le mouvement est mieux aligné avec les concentrations de population et les réseaux de transport par rapport à (une) bien que le nombre total de trajets soit similaire. Cartes préparées par les auteurs à l’aide d’ArcGIS Pro (version 3.0.3, https://www.esri.com/en-us/arcgis) en utilisant les limites administratives du Groupe de la Banque mondiale¹¹ et les données de la simulation décrite.

L’évaluation du mouvement projeté a été réalisée en utilisant la moyenne de dix répétitions pour six configurations différentes (c’est-à-dire, Marshall et al.⁸ modèle avec étalonnage publié, biaisé en faveur de trajets plus courts, et ajustement de notre modèle ; avec le modèle décrit ici et les trois paramétrages), qui ont tous produit un nombre similaire de trajets (1 898 288 ± 555) (voir Informations supplémentaires 1, Fig. S1). En comparant le modèle de gravité et la paramétrisation suggérée par Marshall et al.⁸ il est clair que le mouvement de population projeté (Fig. 3a) est diffus, les petits centres de population étant contournés par des individus au profit de Ouagadougou. Cependant, les résultats du modèle mathématique avec surface de déplacement (Fig. 3b) montrent des déplacements alignés sur la répartition de la population du Burkina Faso (Fig. 3c). De plus, le modèle de gravité semble sous-estimer le nombre de déplacements vers les grands centres de population tout en surévaluant le nombre de déplacements vers les régions peu peuplées. (Fig. 3d). Pour contraster davantage les différences de déplacement, quarante répliques supplémentaires (total n= 50) ont été exécutés pour l’étude de Marshall et al.⁸ modèle avec étalonnage publié, et le modèle décrit ici avec le meilleur ajustement du modèle (voir Informations supplémentaires 2). Les deux modèles produisent des résultats similaires pour les cellules à faible population (c’est-à-dire < 1 000) ; cependant, comme prévu, les modèles divergent considérablement à mesure que la population augmente (voir Informations supplémentaires 1, Fig. S4).

Enfin, lorsque le nombre total de déplacements est comparé à la distance parcourue, les résultats sont également comparables aux données de l’enquête (Fig. 4). Cependant, étant donné la rareté des données d’enquête pour Kourweogo et Bazega (Fig. 4), les déplacements à courte distance projetés sont cohérents avec les données d’enquête et les déplacements à longue distance – qui ont une fréquence globale plus faible, ce qui entraîne moins de répondants à l’enquête – sont généralement cohérents. avec des déplacements similaires hors de la province de Kadiogo. Pour réduire les effets des longues queues de modèle vues dans les deux panneaux inférieurs de la Fig. 4, une valeur alternative de \(log_{e} \left( \rho \right) = 0,45\) a été choisi. La différence était faible avec un peu moins de déplacements vers les centres de population par rapport à la paramétrisation suggérée par Marshall et al. ou la \(log_{e} \left( \rho \right) = 0,20\) valeur (voir Informations supplémentaires 1, Fig. S1, S2).

Les voyages de la providence de Kadiogo se comparent favorablement à ceux de Marshall et al.¹⁷ Enquête sur la base de la distance parcourue. Cependant, les données d’enquête limitées pour Kourweogo et Bazega posent un défi à la validation du modèle, bien que les résultats simulés soient généralement cohérents avec les données d’enquête.